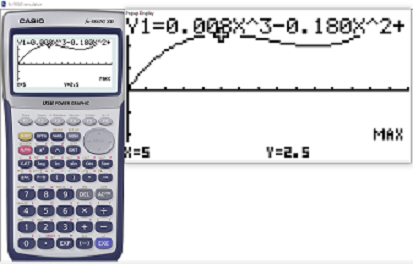
Mathe-Leistungskurs/Lösung zur Prüfung von 2012/2013


Nachfolgend meine Lösungen und Lösungsansätze für die Matheprüfung.


Teil A


1.2.) gk (x) = 4∙e-k∙x → verkettete Funktion → Ableitung mit der Kettenregel


Da u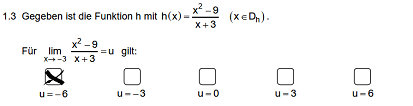ns interessiert Welchen Wert ,,k“ haben muss um auf ½ zu kommen und x=0 ist:
gk´(0)=4e-k∙x∙(-k∙0(0))∙(-k)
gk´(0)=-k∙4e-k∙0 →e0=1
½ = -4k

k=1/8


 











1.4.) Um herauszufinden ob eine Gerade parallel zu einer Ebene ist, prüfe ich hier die Orthogonalität zwischen Normalenvektor der Ebene und Richtungsvektor der Geraden.
Orthogonal bedeutet, dass das Skalarprodukt = 0 sein muss.
(+2)o(-2)
(+1)o(1)
(-6) o (6)

2∙(-2) =-4

-4+ a∙1  = -4+a

-4+a+-6∙6 = -4+a-36

a=40




3.1..) Die Erste Ableitung einer Funktion gibt die Steigung an einer bestimmten Stelle an.
Ist die erste Ableitung 0 so liegt entweder ein Maximum oder ein Minimum vor. Wir bilden also die erste Ableitung der Funktion und setzten diese gleich null
f(x)´ 0= x2-2tx

0=x2(x-2t)

ein Produkt ist Null wenn mindestens einer der Faktoren Null ist...
x1= 02∙(x-2t)
   = 0
x2= x2(0-2t)
   = x2(-2t)
Nun bilden wir, da wir ja wissen das es Extremas gibt, die 2. Ableitung um die y Kordinate des Minimas zu bestimmen
f(x)´´=2x-2t
f´´(0)=0-2t 
Das bedeutet:   
-2t <0  -  lokales Maximum da die Vairiable ,,t" immer größer als Null ist und -2t also immer kleiner als 0
f´´(2t)= 2∙(2t)-2t= 2t - lokales Minmum x=2t
daraus folgt nach Umstellung nach ,,t", dass t= 0,5x ist. das merken wir uns nun für die Lösung der Gleichung vor, setzen jetzt aber erstmal ,,x" in die Gleichung ein, um die Koordinaten des Minimas herauszufinden. (2t)

f(2t)=

1/3 ∙2t3-t∙2t2

=8/3t3-4t3

=-4/3t3
das lokale Minima befindet sich also bei (2t|4/3t3)

Um nun die Gleichung der Geraden aufzustellen die durch das Minima geht, setzen wir einfach die Gerade mit der Funktion gleich und ersetzen den Parameter ,,t" durch das x, welches wir vorhin ausgerechnet haben (t=0,5x).
y= f(x)
y= -4/3t3
y= -4/3∙(0,5x)3
y= -1/6 x3
3.2.)


 1.1) Wieso? Nunja Der Logarithmus ist nur für postive X-Werte definiert, dass heißt die erste,zweite und dritte Antwortmöglichkeit fällt schonmal weg.
Die vierte sieht zwar vielversprechend aus, fällt aber aufgrund der Tatsache das ln 0 nicht definiert ist ebenfalls weg. ( 2∙1,5=3;3-3=0)
Die letzte Antwort ist die einzig richtige Antwort, da hier immer die Elemente in der Klammer  größer als 0 ist.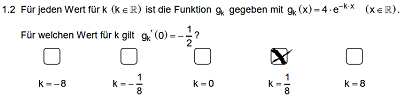














1.3.) Hier fällt es einem auf den Fuß wenn man die binomischen Formeln nicht anwenden kann---man bildet nämlich mithilfe der dritten Binomischen Formel 

(a+b)∙(a-b)=a2-b2

eine neue Gleichung bei der man den Zähler mit dem Nenner kürzen kann

u= lim (x-3)∙(x+3) / x+3

übrig bleibt nun nur noch (x-3 )und man  setzt nun für "x" die "-3" ein.

u= lim (-3-3)

Hiermit kommt man also auf einen Grenzwert von -6











1.5.) Bildung des Normalenvekotrs der Ebene : (1|1|0)
z= 0
da x und y 1 betragen, bedeutet dies, dass der Normalenvektor in der x-y-Ebene liegt, die Ebene an sich also Orthogonal zur x-y Koordinatenebene. (Senkrecht zur z-Ebene kann sie zwar in bestimmten Fällen verlaufen, wir schauen uns aber den allgemeinen Fall für JEDE Ebeneabd an. )???





1.1.) Damit eine Gerade tangential in den den Graphen übergeht, muss der Anstieg beider Funktionen im besagten Punkt P gleich sein.
Weil ich es leid bin das ganze über Word einzutippen nachfolgend handschriftliche Lösungen von mir :




1.2.) Der  größte Durchmesser kann sich an 2 Punkten befinden:
1. Am Maximum der Funktion f(x)- bestimmt über das Grafik-Menü im Taschenrechner.
2. ganz rechts, bei der Funktion g(x)
Also müssen wir nun sowohl schauen, wo wir das Maximum der Funktion f(x) haben und wir setzen den größtmöglichsten Wert für g(x) ein, also 15. (Warum 15?- man kann optisch bereits erkennen, dass 2 Stellen des Rotationskörper höher als der Rest sind. Das beruht also auf eine rein logische Überlegung.)



Das Maximum der Funktion f(x) inb diese´m Intervall befindet sich also bei(5|2,5).
Nun prüfen wir das noch bei der Funktion g(x) indem wir 15 einsetzen.
0,144∙15+0,484= 2,644

2,644>2,5
Das Maximum liegt also bei 15|2,644

Um nun aber den Durchmesser in Zentimetern herauszufinden, müssen wir das Ergebniss noch mal zwei rechnen, da wir ja nur eine Hälfte des Werkstückes betrachtet haben

2,644∙2=5,288
Der größte Durchmesser beträgt also 5,288cm.




1.3.) Anhand unserer bisherigen Rechnungen wissen wir nun 2. Dinge:
die Funktion f(x) liegt im Intervall 0<=x<=11
und die Funktion g(x) im Intervall 11<=x<=15
zur weiteren Berechnung brauchen wir nun, da es sich um einen Rotationskörper handelt, der um die x- Achse dreht , die entsprechende Formel dafür die folgendermaßen lautet:
 V = π ⋅ ∫  ( f ( x ) )2  d x
das bedeutet wir Quadtrieren unsere Funktion und bilden danach das Integral davon.
Dies machen wir für beide Funktionen, denn das Gesamtvolumen setzt sich aus beiden Funktionen zusammen f(x) in den Grenzen (0|11) addiert mit  g(x) in den Grenzen (11|15)
π∙0∫11 (f(x))2=
-0,000064∙116-0,00288∙115+0,0516∙114-0,432∙113+1,44∙112
=47.517π
= 149,279
π∙11∫15(g(x))2
Rechenhinweis:obere- untere Grenze
π(1/3∙0,020736∙153+1/2∙0,13939∙152+0,23426∙15)
= 42,523π
42,523π - π(1/3∙0,020736∙113+1/2∙0,13939∙112+0,23426∙11)
= 22,313π
= 70,099
149,279cm3+70,099cm3=219,378cm3
Masse des Gesamtstücks berechnet sich aus Volumen in

cm3 ∙ 0,8g/cm3
219,378cm3∙ 0,8g/cm3=175,79g
Nun müssen wir noch die Masse des zylinderförmigen Hohlraums errechnen. Von diesem wissen wir dass er 10cm tief ist und einen Durchmesser von 3cm (r=1/2∙3cm=1,5cm) besitzt. Das Tafelwerk gibt uns folgende Formel zur Berechnung von Zylindern an:
π∙r2∙h
π∙1,5cm2∙10cm
=22,5cm3π
= 70,686cm3
nun berechnen wir die Masse des Hohlraums und ziehen diese von der Gesamtmasse ab, da der Hohlraum ja ausgebohrt wurde.
Masse Hohlraum= 70,686cm3∙0,8g/cm3
=56,549g
175,79g-56,549g=119,24g


1.4.)

Zur Lösung der Aufgabe ist e gut zu wissen, dass wir zur Berechnung des Durchmessers eine Gerade bilden müssen die folgende 3 Bedingungen erfüllt:

1. Sie geht durch den Punkt R

2. Minimales Verpackungsvolumen= Verpackung muss den Rotationskörper am Maximum ,,tangieren"

3. Anstieg der Geraden mit der Funktion muss übereinstimmen
































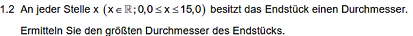Folgende 2 Stellen kommen für die Ermittlung in Frage: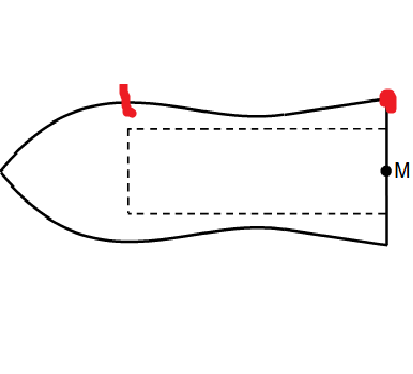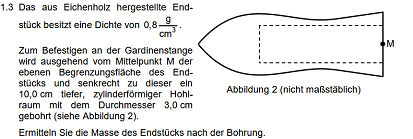
Aufgabe 2 Teil B



2.1.) Das Dreieck ABC ist gleichschenklig wenn zwei der drei Seiten die selbe Länge besitzen.
Hierfür habe ich mir eine Skizze angefertigt und dann den Betrag der Seite AB mit der Seite BC verglichen.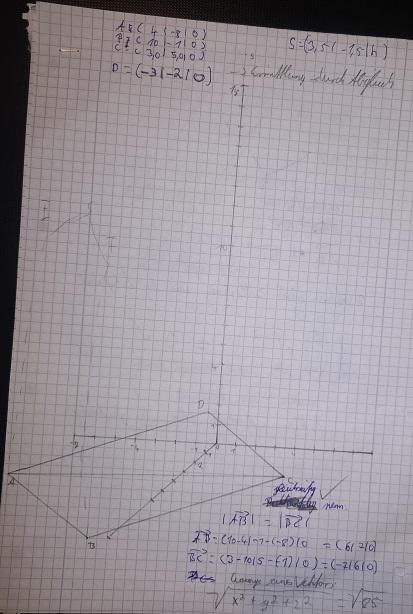
Um nun zu überprüfen ob das Dreieck auch rechtwinklig ist, bildet man nun von diesen beiden Seiten das Skalarprodukt.Dieses muss 0 ergeben.

Punkt D lässt sich nun, da es sich um eine quadratische Grundfläche handelt, einfach über Abgleichen der anderen Punkte ermitteln.




2.2.)



,,Paralelle Ebenen unterscheiden sich nur in der Variable ,,d" "

Diese mathematische Grundlage hilft uns in unsererer weiteren Vorgehensweise.:

Zuallerst stellen wir die Ebenengleichung für die Ebene BCGF auf. Ich nehme hierfür den Ortsvektor OB und die Spannvektoren OF und OC.

Im 2. Schritt formen wir nun nach der Hesseschen Normalform um und bilden hierfür den Normalenvektor. Hierfür bilde ich das Kreuzprodukt aus den 2 Spannvektoren.

3. Schritt: Um nun ,,d" für den Normalenvektor herauszubekommen, setze ich einfach irgendeinen Punkt ein, welcher in der Ebene liegt. Bei mir ist dies ;,B". Das  VEREINFACHTE (:18) Ergebnis beträgt 53. Dieses Ergebnis merken wir uns erstmal vor und berechnen nun einen Punkt der gesuchten Ebene. Hierfür multiplizieren wir einfach den Einheitsvektor mit einem beliebigen Punkt in unserer bereits gegebenen Ebene, welcher in Richtung des Vektors AB liegt ich nehme hierfür ,,B"

4. Schritt: Ich setze diesen Punkt in die Koordinatenform meiner Ebene BCGF ein um ,,d" herauszubekommen












































































































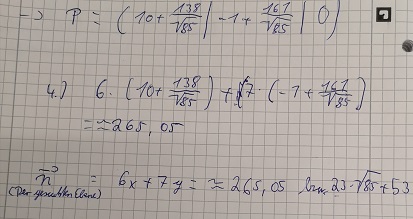GESCHAFFT!